This paper synthesizes research on integrating problem posing into mathematics education, exploring questions such as the nature of teaching mathematics through problem posing, defining its tasks, guiding teachers on handling student-generated problems, supporting teacher learning in this approach, and assessing the impact of Problem-Posing-Based Learning (P-PBL) on both teachers and students. The author raises additional unanswered questions and proposes a P-PBL instructional model, aiming to inspire further scholarly engagement in problem-posing research for enhanced mathematics learning opportunities.
Introduction:
In 2003, I synthesized key research findings on teaching mathematics through problem solving, addressing concerns such as whether young children can independently explore and solve problems, how teachers can learn this approach, students’ beliefs about it, and potential sacrifices in basic skills. The paper was a counterpart to a previous one on Problem-Based Learning (PBL). The current paper, a “sister paper,” focuses on Problem-Posing-Based Learning (P-PBL), reflecting the growing emphasis on integrating problem posing into education to enhance students’ mathematical learning through engaging activities. This research highlights the need for further studies to comprehensively address the issues raised in both teaching methodologies.
Why problem posing?
The significance of problem posing in scientific discovery has been emphasized, as highlighted by Einstein’s assertion that formulating a problem can be more crucial than solving it. This concept is exemplified by David Hilbert’s influential set of mathematical problems. Problem posing in science and education, especially in mathematics, has been acknowledged as a vital intellectual activity.
The paper focuses on Problem Posing-Based Learning (P-PBL) in mathematics education, asserting its theoretical soundness based on constructivist and sociocultural perspectives. P-PBL is seen as a way to enhance students’ access to mathematical sensemaking and learning by allowing them to formulate their own problems, bridging existing and new mathematical understandings.
Despite the cognitive demands, problem-posing activities can be adapted to various student levels, providing a learning approach with a low entry barrier and high potential. Students engaging in problem posing not only become active contributors but also develop positive mathematical identities.
The need for a deeper understanding of teaching mathematics through problem posing is recognized, with researchers exploring frameworks, learning cycles, and strategies for effective implementation. Previous studies have laid the groundwork, offering insights into task organization, student dynamics, and teacher interventions.
The paper aims to synthesize existing research on teaching mathematics through problem posing, addressing questions about its nature, tasks, and the impact on both teachers and students. While not exhaustive, the review intends to shed light on the promises and challenges associated with this instructional approach, emphasizing the complexity of classroom instruction and the need for continued exploration in the field.
A P-PBL instructional model :
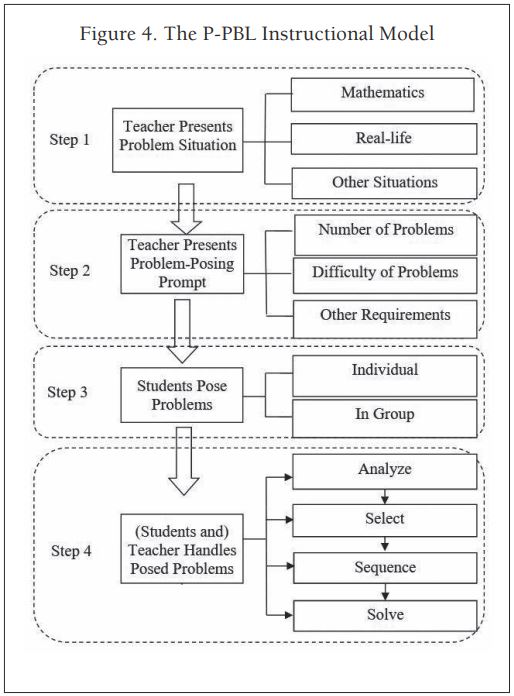
The proposed P-PBL (Problem Posing within Problem-Based Learning) instructional model focuses on using problem-posing tasks as a unit of interest for teaching mathematics. This model comprises four steps: (a) the teacher presents a problem-posing situation, (b) the teacher provides a problem-posing prompt, (c) students pose problems individually or in groups, and (d) teachers handle the posed problems based on learning goals. The first two steps are usually presented together, emphasizing the importance of considering both situations and prompts in planning. Problem-posing situations can be mathematical or real-life, related to students’ interests. Step 3 involves students posing problems, though understanding the cognitive processes remains a challenge.
Step 4 suggests instructional practices (analyze, select, sequence, solve) to handle posed problems, reinforcing learning through solving some of them. The analyze practice involves categorizing and clarifying posed problems, guiding students to correct errors and convey criteria for good problems. Selection is based on difficulty and relevance, encouraging variety for diverse learning opportunities. Sequencing is vital, ensuring a pedagogically sensible order for solving problems. The solve practice draws on established methods for teaching mathematics through problem solving.
The P-PBL model guides mathematics teaching through problem posing, supported by existing teaching cases. Further research is needed to verify and refine the model, especially in Step 4, detailing how to analyze, select, and sequence posed problems. The paper encourages scholars to engage in problem-posing research to enhance opportunities for students to learn mathematics through this approach.
Source:
Cai, J. (2022). What Research Says About Teaching Mathematics Through Problem Posing. Education & didactique, 16, 31-50. https://doi.org/10.4000/educationdidactique.10642
 Canadian Academy Discover, Publish, Thrive
Canadian Academy Discover, Publish, Thrive